In this post we will solve the question diagonal difference from hackerrank in golang. We will learn how to create and use a 2-D matrix in Golang and how to traverse over it. Let's get started.

Problem Statement

The question can be found at this link. The problem statement states that we need to calculate the absolute difference of sum of elements of left and diagonal of a square matrix(a 2-D array whose rows and columns length are same).

Couple of things to note here is

• We need to take the size of the matrix as input
• In golang array length are fixed
• Logic to deduce if an element belongs to left, right or none of the diagonals
• Some way to calculate absolute difference
• we are solving this in golang (assuming you have either seen my previous posts or are comfortable with basics of golang. In case you need a refresher, refer to my older posts.)

Challenges

• Choose our preferred language as golang on hackerrank. The moment we do that, we get some 50-60 lines of code which are very unfamiliar to someone who is new to language.
• To solve the problem we need to know couple of things
• To declare a 2-D array
• To take inputs for the matrix
• Deduce the logic to determine if a given element belongs to left or right diagonal
• Doing the calculations required to get to our desired output

Solution

This is the template you get on hackerrank for this problem statement.

    package main

    import (
        "bufio"
        "fmt"
        "io"
        "os"
        "strconv"
        "strings"
    )

    // Complete the diagonalDifference function below.
    func diagonalDifference(arr [][]int32) int32 {


    }

    func main() {
        reader := bufio.NewReaderSize(os.Stdin, 1024 * 1024)

        stdout, err := os.Create(os.Getenv("OUTPUT_PATH"))
        checkError(err)

        defer stdout.Close()

        writer := bufio.NewWriterSize(stdout, 1024 * 1024)

        nTemp, err := strconv.ParseInt(readLine(reader), 10, 64)
        checkError(err)
        n := int32(nTemp)

        var arr [][]int32
        for i := 0; i < int(n); i++ {
            arrRowTemp := strings.Split(readLine(reader), " ")

            var arrRow []int32
            for _, arrRowItem := range arrRowTemp {
                arrItemTemp, err := strconv.ParseInt(arrRowItem, 10, 64)
                checkError(err)
                arrItem := int32(arrItemTemp)
                arrRow = append(arrRow, arrItem)
            }

            if len(arrRow) != int(n) {
                panic("Bad input")
            }

            arr = append(arr, arrRow)
        }

        result := diagonalDifference(arr)

        fmt.Fprintf(writer, "%d\n", result)

        writer.Flush()
    }

    func readLine(reader *bufio.Reader) string {
        str, _, err := reader.ReadLine()
        if err == io.EOF {
            return ""
        }

        return strings.TrimRight(string(str), "\r\n")
    }

    func checkError(err error) {
        if err != nil {
            panic(err)
        }
    }

• First go ahead and delete everything in the pre-existing template.
• Replace it with the template that we have been following till now.

Now your code should look something like this

    package main
    
    import (
        "fmt"
    ) 

    func main(){
        
    }

First thing we need is to make sure is that we have a variable to take the matrix size as input. So let's declare a variable and take a input.

    var n int
    fmt.Scan(&n)

Now comes the interesting part.

Multi Dimensional Arrays in Golang

If you remember from our previous posts, we declared an array using var a [3]int, so you must be thinking, that is good enough, we will declare a 2-D matrix using var a [n][n]int right? WRONG!!! If you notice in the first case, the number inside the square brackets, is a constant, it's a number. The value of 3 won't change, it will always be 3. But in second case, we are giving the length n, which is a variable. In golang the length of an array needs to be fixed, a constant. It cannot be a variable.

Now you must be thinking, let's go ahead and change var to const to make sure n is a constant. That would have worked if we had assigned the value of n while declaring it, but that is not the case. We need to take it as an input in the next line. Const requires you to initialize your constants at the time of creation. So in simple terms we can't make n a constant, and we can't use [][] syntax here. Can we do something else? Yes, we will use make to allocate memory for our array. Let's see how we can do this.

    ...
    a := make([][]int, n)
    

In the above code snippet, we are creating a 2-D array a of int type, and stating that it will hold n number of rows. We have just allocated the memory for n rows, we still have to specify number of columns for each row and allocate memory for it. Somehow we need to loop over the number of rows, and for each row allocate n columns of memory. So at this point of time it is pretty clear that , we are going to loop over the rows, now can we just create another inner loop to loop over columns, take each input and do our calculations? Yes we can, and that is exactly what we are going to do.

    ...
    lsum,rsum := 0,0
    for i:=0;i<n;i++{
        a[i] = make([]int,n)
        for j:=0;j<n;j++{
            fmt.Scan(&a[i][j])
            // calculate lsum here
            // calculate rsum here    
        }
    } 

Okay, here we have a bunch of code, let's start exploring what they mean. On the first line, I am declaring and initializing two variables to store our left diagonal and right diagonal sum. Next we are looping over the number of rows and allocating memory for n columns for each row of the matrix. Again we are using make to allocate memory and are specifying that a[i] will be an array of int type of length n. Next we are looping over the number of columns for each row. Now that we have successfully created our nested loops which would traverse over the matrix in the order that we want, we are ready to take inputs for each index. Next we are taking inputs for each index. Now we will write the logic to determine if the element belongs to left diagonal or right diagonal and add it to correct variable accordingly.

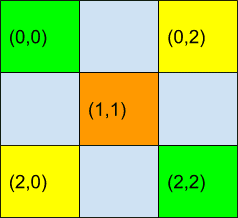
Left and Right Diagonals

Refer the picture below, and forgive me for my bad drawing, still learning how to use some of the drawing tools

The elements in green and brown are the elements that belong to left diagonal, while the element which are in yellow and brown belong to the right diagonal. Notice the indexing in the boxes, if you look the indexes for the left diagonal, both the row number and the column number are same. Here we got our first condition to determine if an element belongs to left diagonal. For the right diagonal, if you notice, the sum of the indexes are always 2 in our case, I want you to try it out for other higher order matrix, say 4*4 matrix. You'll notice that it always equal to size - 1 of matrix. Now we got both of our conditions to determine the elements of left and right diagonal. Let's replace the comments with original sum logic

    ...
    if i==j {
        lsum += a[i][j]
    }
    if i+j == n-1 {
        rsum += a[i][j]    
    }

Now that we have our sum in place we need absolute difference of these two sums. To calculate absolute difference we need couple of things

• math package from golang
• Abs function from package math
• The difference of lsum and rsum in float64

So we will use Abs function from math package to get absolute difference of lsum and rsum and Abs function take float64 as argument, so we need some type casting on the original difference. Let's look at steps. We will add these after our nested for loops

    ...
    diff := math.Abs(float64(lsum-rsum))
    fmt.Println(diff)

Very simple steps here, we taking difference of lsum and rsum, we could have done it vice-versa too, since we need absolute value, the order doesn't matter. We are then type casting it to float64 and calling Abs function . Then assigning the result to diff and printing it. Now we are using a new library here math, so we need to import it here. Change our import statement to

    ...
    import(
        "fmt"
        "math"
    )
    ...

Now that we have completed our code, the complete one should look like

    package main

    import (
        "fmt"
        "math"
    )

    func main(){

        var n int
        fmt.Scan(&n)

        a := make([][]int, n)

        lsum,rsum := 0,0

        for i:=0;i<n;i++{
            a[i] = make([]int,n)
            for j:=0;j<n;j++{
                fmt.Scan(&a[i][j])
                if i == j {
                    lsum += a[i][j]
                }
                if i+j == n-1 {
                    rsum += a[i][j]
                }
            }
        }

        diff := math.Abs(float64(lsum - rsum))
        fmt.Println(diff)


    }

We learned a lot of good stuff in this one, and we are definitely making good progress on our hackerrank golang journey. That's it for this one. See you in the next one.

There you go guys, you made it to the end of the blog. Please check out the video below if you still have any doubts. Subscribe to my youtube channel and my mailing list below for regular updates. Follow me on twitter , drop me a mail or leave a comment here if you still have any doubts and I will try my best to help you out. Thanks

Stay tuned and see you around :)